Question

Perform a one-sample 2-test for a population mean using the P-value approach. Be sure to state the hypotheses and the significance level, to compute the value of the test statistic, to obtain the P-value, and to state your conclusion.

In the past, the mean running time for a certain type of flashlight battery has been 8.3 hours. The manufacturer has introduced a change in the production method which he hopes has increased the mean running time. The mean running time for a random sample of 40 light bulbs was 8.5 hours. On the data provide sufficient evidence to conclude that the mean running time of all light bulbs, j, has increased from the previous mean of 8.3 hours? Perform the appropriate hypothesis test using a significance level of 0.05. Assume that a 0,5 hours

Answer 1

The p-value of 0.0057 is less than the significance level (α=0.05). Therefore, we reject the null hypothesis.

A one-sample z-test to determine whether there's sufficient evidence to conclude that the mean running time of all light bulbs has increased from the previous mean of 8.3 hours.

Here are the steps:

Hypotheses:

Null Hypothesis (H0): The mean running time (μ) is equal to 8.3 hours.

Alternative Hypothesis (H1): The mean running time (μ) is greater than 8.3 hours.

Given data:

Population mean (μ): 8.3 hours (from the past)

Sample mean (x ): 8.5 hours

Sample size (n): 40

Assumed population standard deviation (σ): 0.5 hours

Significance level:

α=0.05

Test statistic formula for one-sample z-test:

`Z= (x- \mu)/((\sigma)/(√(n) ) )`

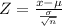
​Where:

x = Sample mean

μ = Population mean under the null hypothesis

σ = Population standard deviation

n = Sample size

Calculations:

Z= 8.5−8.3/ 0.5/ √40

​Z= 0.2 /0.5/√40

​Z= 0.2/ 0.0791

Z≈2.528

P-value:

Using a z-table or a statistical calculator, we find that the p-value corresponding to Z=2.528 is approximately 0.0057.

The p-value of 0.0057 is less than the significance level (α=0.05). Therefore, we reject the null hypothesis. There is sufficient evidence to conclude that the mean running time of all light bulbs has increased from the previous mean of 8.3 hours at a 5% level of significance.