In a standard normal distribution with mean 0 and standard deviation 1, the value of
 for
for
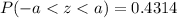 is approximately
is approximately
 , encompassing 43.14% of the distribution's area between
, encompassing 43.14% of the distribution's area between
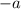 and
and
 .
.
Given that
 scores are normally distributed with a mean of 0 and a standard deviation of 1, and the probability
scores are normally distributed with a mean of 0 and a standard deviation of 1, and the probability
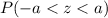 = 0.4314 , we'll use the properties of the standard normal distribution to find
= 0.4314 , we'll use the properties of the standard normal distribution to find
 .
.
For a standard normal distribution, the area between
 and
and
 under the curve represents the probability
under the curve represents the probability
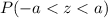 .
.
Given
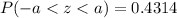 , we want to find the value of
, we want to find the value of
 .
.
From the properties of symmetry in the standard normal distribution, the total area between
 and
and
 is
is
 , which corresponds to the probability
, which corresponds to the probability
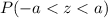 .
.
Given:
![\[ P(-a < z < a) = 0.4314 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/t67e80b77hfepdv8sshfdrxru4e2qp6rkq.png)
Since the total area is
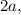 and
and
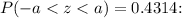
![\[ 2a = 0.4314 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bvxyuwrmvnvio0nn2gq2htb2o2g00ceedk.png)
![\[ a = (0.4314)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/urzynh4x2q5mt1pg16q6krdglmgzvhjssp.png)
![\[ a = 0.2157 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/88s0zoas1dbjjgep4tqhpf9mdka9yo0qdm.png)
Therefore, the value of
 such that
such that
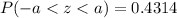 in a standard normal distribution is approximately
in a standard normal distribution is approximately

complete the question
Assume that z scores are normally distributed with a mean of 0 and a standard deviation of 1. If P (-a < z < a) = 0.4314, find a.