The constant torque required to stop the counterclockwise-spinning flywheel with a radius of 1.18 m, mass 94.6 kg, and initial angular velocity 443 rpm in 1.00 minute is approximately -51.37 N·m.
To calculate the constant torque required to stop the flywheel in 1.00 minute, we can use the rotational analog of Newton's second law:
![\[ \tau = I \alpha \]](https://img.qammunity.org/2024/formulas/physics/high-school/giyd9oy92wi3ykvng94y63zqstru17xnpc.png)
where:
-
 is the torque,
is the torque,
- \(I\) is the moment of inertia of the flywheel,
-
 is the angular acceleration.
is the angular acceleration.
The moment of inertia \(I\) for a uniform disk is given by:
![\[ I = (1)/(2) m r^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/f3gamvv4jq377539zvi6suzqfkq1fngfz7.png)
where:
-
 is the mass of the flywheel,
is the mass of the flywheel,
-
 is the radius of the flywheel.
is the radius of the flywheel.
The angular acceleration
 can be calculated from the angular velocity
can be calculated from the angular velocity
 using the equation:
using the equation:
![\[ \alpha = (\Delta \omega)/(\Delta t) \]](https://img.qammunity.org/2024/formulas/physics/college/83fngy8shim7782fp3gcp9z8o3e04ogr5v.png)
The change in angular velocity
 is given by the final angular velocity
is given by the final angular velocity
 (when the flywheel stops) minus the initial angular velocity
(when the flywheel stops) minus the initial angular velocity
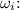
![\[ \Delta \omega = \omega_f - \omega_i \]](https://img.qammunity.org/2024/formulas/physics/high-school/jpfwb8owxogmfjxqes4277oijg7o59egk4.png)
The final angular velocity
 is 0, as the flywheel comes to a stop.
is 0, as the flywheel comes to a stop.
Let's plug in the given values and calculate the torque:
Given data:
- Radius
 = 1.18 m
= 1.18 m
- Mass
 = 94.6 kg
= 94.6 kg
- Initial angular velocity
 = 443 rpm
= 443 rpm
- Time
 = 1.00 min
= 1.00 min
First, convert the initial angular velocity to radians per second:
![\[ \omega_i = \frac{443 \, \text{rpm} * 2 \pi \, \text{rad}}{60 \, \text{s}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/k64psslrootzuoep0hdf2tm1dgg4j3f23g.png)
Then, calculate the angular acceleration:
![\[ \alpha = (-\omega_i)/(t) \]](https://img.qammunity.org/2024/formulas/physics/high-school/p5hhd3evlsupwp10bxkfl7u1j02qetc6sy.png)
Finally, use the torque equation to find the constant torque:
![\[ \tau = I \alpha \]](https://img.qammunity.org/2024/formulas/physics/high-school/giyd9oy92wi3ykvng94y63zqstru17xnpc.png)
![\[ \tau = (1)/(2) m r^2 \alpha \]](https://img.qammunity.org/2024/formulas/physics/high-school/rq8eytdjsu73i335osjo0q7kx6bg9r8gg3.png)
Now, let's proceed with the calculations:
1. Convert
 to radians per second:
to radians per second:
![\[ \omega_i = (443 * 2 \pi)/(60) \, \text{rad/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/odo2zmmsrkggrvih34nhocj4gh44zefp9l.png)
2. Calculate \(\alpha\):
![\[ \alpha = (-\omega_i)/(t) \]](https://img.qammunity.org/2024/formulas/physics/high-school/p5hhd3evlsupwp10bxkfl7u1j02qetc6sy.png)
3. Calculate \(I\) using the moment of inertia formula:
![\[ I = (1)/(2) m r^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/f3gamvv4jq377539zvi6suzqfkq1fngfz7.png)
4. Plug in the values into the torque formula:
![\[ \tau = I \alpha \]](https://img.qammunity.org/2024/formulas/physics/high-school/giyd9oy92wi3ykvng94y63zqstru17xnpc.png)
Now, let's perform the calculations.
1. Convert
 to radians per second:
to radians per second:
![\[ \omega_i = (443 * 2 \pi)/(60) \, \text{rad/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/odo2zmmsrkggrvih34nhocj4gh44zefp9l.png)
![\[ \omega_i \approx 46.32 \, \text{rad/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/lpiesehr9isdzb4olr1lmylsmy3zn0vknw.png)
2. Calculate
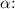
![\[ \alpha = (-\omega_i)/(t) \]](https://img.qammunity.org/2024/formulas/physics/high-school/p5hhd3evlsupwp10bxkfl7u1j02qetc6sy.png)
![\[ \alpha = (-46.32)/(60) \, \text{rad/s}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/ye3i07e7xkawke9cjpjp9wf62qbr4hu5f3.png)
![\[ \alpha \approx -0.772 \, \text{rad/s}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/z9x8hghddffivraf8xtya2aj3wz6h22yw2.png)
3. Calculate \(I\) using the moment of inertia formula:
![\[ I = (1)/(2) m r^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/f3gamvv4jq377539zvi6suzqfkq1fngfz7.png)
![\[ I = (1)/(2) * 94.6 * (1.18)^2 \, \text{kg} \cdot \text{m}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/6colqf0cqul81oe4m7i1fsvnjo7r8uoxjh.png)
![\[ I \approx 66.52 \, \text{kg} \cdot \text{m}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/rxh3qe5y62wndocls2uz2z5y4e46xdf9gz.png)
4. Plug in the values into the torque formula:
![\[ \tau = I \alpha \]](https://img.qammunity.org/2024/formulas/physics/high-school/giyd9oy92wi3ykvng94y63zqstru17xnpc.png)
![\[ \tau = 66.52 * (-0.772) \]](https://img.qammunity.org/2024/formulas/physics/high-school/l7zsczgeanoegxpcps5lay4kz0jhumzucf.png)
![\[ \tau \approx -51.37 \, \text{N} \cdot \text{m} \]](https://img.qammunity.org/2024/formulas/physics/high-school/pfamgk3qpejvhx7ysxbcczq5n74smaefcg.png)
The constant torque required to stop the flywheel in 1.00 minute is approximately
 The negative sign indicates that the torque is acting in the opposite direction of the initial rotation, which is counterclockwise.
The negative sign indicates that the torque is acting in the opposite direction of the initial rotation, which is counterclockwise.