Question

if the estimated number of steps needed to reach 0 from n is n² what is the probability that 0 will not be reached

Answer 1

The probability that 0 will not be reached in
`n^2` steps approaches
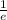`(1)/(e)` or approximately 0.3679.

If the estimated number of steps needed to reach 0 from n is
`n^2` , it implies that the probability of not reaching 0 within
`n^2` steps can be determined.

Let's consider the probability of not reaching 0 in a single step from a specific n to n−1. This probability is
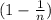`(1- (1)/(n) )` ​because there's only one way to reach n−1 (by decrementing from n), out of n possible numbers (including 0).

Now, for n steps, the probability of not reaching 0 is

`(1- (1)/(n) )^n`

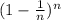
This can be thought of as the probability of not reaching 0 in a single step, repeated n times.

For
`n^2` steps, the probability of not reaching 0 is
`(1- (1)/(n) )^n^2`

This probability tends to
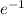`e^(-1)` (where e is the base of the natural logarithm) as n becomes large.

So, the probability that 0 will not be reached in n^2 steps approaches
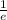`(1)/(e)` or approximately 0.3679.