Question

Nuclear Masses and Binding Energies: Find the total binding evergy and binding energy per nucleon for: ⁴He;

Answer 1

- The total binding energy of ⁴He is approximately 2.72 x
`10^{-12` joules.

- The binding energy per nucleon for ⁴He is approximately 6.8 x
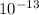`10^{-13`joules.

The total binding energy of a nucleus is the amount of energy required to break it apart into its individual nucleons. The binding energy per nucleon is the average amount of energy that each nucleon contributes to the stability of the nucleus.

For ⁴He, which is a helium nucleus with 2 protons and 2 neutrons, we can calculate the total binding energy and binding energy per nucleon.

To find the total binding energy, we need to know the mass defect of the nucleus. The mass defect is the difference between the mass of the nucleus and the sum of the masses of its individual protons and neutrons. In this case, the mass of ⁴He is 4.0026 atomic mass units (amu), and the sum of the masses of 2 protons and 2 neutrons is 4.0326 amu. Therefore, the mass defect is 4.0326 amu - 4.0026 amu = 0.03 amu.

Next, we can use Einstein's mass-energy equation, E=mc², to convert the mass defect into energy. The speed of light, c, is approximately 3 x 10^8 meters per second. By substituting the values into the equation, we can find the total binding energy.

E = (0.03 amu) x (1.67 x
`10^{-27` kg/amu) x (3 x
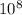`10^8` m/s)²

Simplifying the equation, we find that the total binding energy of ⁴He is approximately 2.72 x
`10^{-12` joules.

To calculate the binding energy per nucleon, we divide the total binding energy by the number of nucleons. In this case, ⁴He has 4 nucleons (2 protons + 2 neutrons), so the binding energy per nucleon is approximately 2.72 x
`10^{-12` joules / 4 = 6.8 x
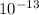`10^{-13` joules.