Question

A small college has \[800\] students, \[10\%\] of which are left-handed. Suppose they take an of \[8\] students. Let \[L=\] the number of left-handed students in the sample. Which of the following would find \[P(L=2)\]? Choose 1 answer: Choose 1 answer: (Choice A) \[\displaystyle{800 \choose 8}(0.10)^2(0.90)^6\] A \[\displaystyle{800 \choose 8}(0.10)^2(0.90)^6\] (Choice B) \[\displaystyle{8 \choose 2}(0.10)^6(0.90)^2\] B \[\displaystyle{8 \choose 2}(0.10)^6(0.90)^2\] (Choice C) \[\displaystyle{8 \choose 2}(0.10)^2(0.90)^6\] C \[\displaystyle{8 \choose 2}(0.10)^2(0.90)^6\] (Choice D) \[(0.10)^6(0.90)^2\] D \[(0.10)^6(0.90)^2\] (Choice E) \[(0.10)^2(0.90)^6\] E \[(0.10)^2(0.90)^6\]

Answer 1

Therefore, the correct choice to find (P(L=2)) is (Choice C)
`\(\binom{8}{2} * (0.10)^2 * (0.90)^6\).`

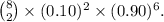
How to get the right option

To find P(L=2) (the probability of getting 2 left-handed students in a sample of 8), we use the binomial probability formula, which is

`\(P(X=k) = \binom{n}{k} \cdot p^k \cdot q^(n-k)\)`,

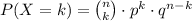where n is the number of trials, k is the number of successes, p is the probability of success, and q is the probability of failure.

Here, n = 8 (the sample size), k = 2 (the number of left-handed students we want), p = 0.10 (probability of selecting a left-handed student),

q = 1 - p

1 - 0.10

= 0.90

(probability of not selecting a left-handed student).

Therefore, the correct choice to find (P(L=2)) is

(Choice C)

`\(\binom{8}{2} * (0.10)^2 * (0.90)^6\).`

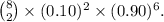
question

The complete question is in the attachment