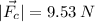Answer:
a)
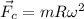
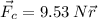
b)
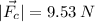
Explanation:
a) The centripetal force equation is:
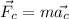
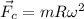
Now, we know that the body makes one revolution every 5 seconds, so we can find the angular velocity:
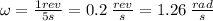
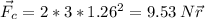
The centripetal force is a vector in the radius direction.
b) The magnitude of that force will be: