Question

a body of mass (4 m) is lying in x-y plane at rest. it has suddenly explodes into three pieces. two pieces, each of mass (m) move perpendicular to each other with equal speeds (v). the total kinetic energy generated due to explosion is :

Answer 1

The total kinetic energy generated due to explosion is
`(3)/(2)mv^(2)`

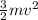
The third fragment has the same mass (m) as the other two and moves in a direction perpendicular to both of them (forming a right triangle with u and v as the two legs), then its kinetic energy would also be =

1/2 * m * v²

We squaring both sides of u² + v² = u² + v² = 2u²

the total velocity is the hypotenuse and u is one leg

v = √(u²).

we then have that the third fragment's kinetic energy would be :

1/2 * m * (√(u²))² = mu²

we then adding the kinetic energies of all three fragments:

`= 2 * (1/2 * m * u^2) + 1/2 * m * u^2 \\= 3 * (1/2 * m * u^2) \\= 3/2 mv^2.`