Question

A small glass ball is pushed with a speed V from A. It moves on a smooth surface and collides with the wall at B. If it loses 1/3rd of the speed during the collision, find the average speed and average velocity of the ball till it reaches at its initial position

Answer 1

a. The average speed of the ball is =
`(S)/(t_1)`

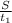
b. The average velocity of the ball = 0

We use the formula

v² = u² + 2as

v = the final speed (2/3 * V)

u = the initial speed (V)

a = the acceleration (negative due to deceleration)

s= the distance traveled (distance from A to B)

`t_1`= s / V found from the equation

The collision is assumed to be elastic , the speed after rebounding from the wall (v) will be the same as before the collision (2/3 * V). The ball travels the same distance back to point A, so the time taken to return will also be equal to
`t_1.`

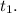
Average speed:

`(2s) / (t_1 + t_2) \\= (2s) / (2t_1) \\= s / t_1`

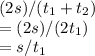
b.

Average velocity is described as the displacement divided by the total time taken. Since the ball returns to its initial position, the displacement is 0.

Average velocity =
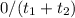
`0 / (t_1 + t_2)`

= 0 / (
`2t_1`)

= 0