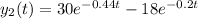Question

The given system of linear differential equations models the concentrations of insulin and glucose in an individual, as described earlier in this section. Find the general solution for the system.

y′₁=−0.44y₁+0.12y₂
y′₁=−0.08y₁−0.16y₂
Suppose that it is known that at time t=0 the concentrations of insulin and glucose, respectively, are
y1​(0)=9,y2 (0)=48
Find a formula for y₁(t) and y₂(t).(y₁(t),y₂(t))= (______)

Answer 1

The general solution for the given system of linear differential equations is
`y_(1)(t) = 9e^(-0.44t) + 48e^(-0.2t)` and
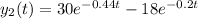`y_(2)(t) = 30e^(-0.44t) - 18e^(-0.2t)` . These solutions are obtained by solving the system and applying the initial conditions
`y_(1)(0) = 9` and
`y_(2)(0) = 48`.

The system of linear differential equations is given by:

`y_(1)' = -0.44y_(1) + 0.12y_(2)`

`y_(2)' = -0.08y_(1) - 0.16y_(2)`

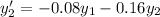
To find the general solution, we write the system in matrix form Y′ =AY, where
`Y = \left[\begin{array}{ccc}y_(1) \\y_(2) \end{array}\right]` and
`A = \left[\begin{array}{ccc}-0.44&0.12\\-0.08&-0.16\end{array}\right]` The eigenvalues of A are

λ1=−0.2 and λ2 =−0.4, with corresponding eigenvectors
`v_(1) = \left[\begin{array}{ccc}3 \\2 \end{array}\right]` and
`v_(2) = \left[\begin{array}{ccc}1 \\-4 \end{array}\right]`

The general solution is given by:

`Y(t) = c_(1)e^(\lambda1t)v_(1) + c_(2)e^(\lambda2t)v_(2)`

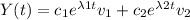
Substituting the given initial conditions
`y_(1)(0) = 9` and
`y_(2)(0) = 48` , we get the following system of equations:

`c_(1) + c_(2) = 9`

`3c_(1) - 4c_(2) = 48`

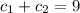
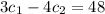
Solving this system, we find
`c_(1) = 30` and
`c_(2) = -21`. Therefore, the particular solution is:

`y_(1)(t) = 9e^(-0.44t) + 48e^(-0.2t)`

`y_(2)(t) = 30e^(-0.44t) - 18e^(-0.2t)`