Question

Find the laplace transform of f (t)
f(t) = t sin 3t

Answer 1

The Laplace transform of f(t)=t⋅sin(3t) is
`(3)/((s^2+9)^2).`

The Laplace transform of a function f(t) is given by:

L{f(t)}=
`\int\limits^a_0 {e^(-st)} f(t)dt,`

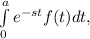
where s is a complex number parameter.

Let's find the Laplace transform of

f(t)=tsin(3t):

Firstly, recall that the Laplace transform of ⋅sin(at) (where n is a non-negative integer) is given by:

`L{t^n. sin(at)}= (n!.a)/((s^2+a^2)^(n+1))`

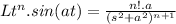
In this case, n=1 and a=3. Thus, the Laplace transform of t⋅sin(3t) is:

`L{t^n. sin(3t)}= (1!.3)/((s^2+3^2)^(3+1)) =(3)/((s^2+9)^2)`

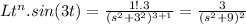
Therefore, the Laplace transform of f(t)=t⋅sin(3t) is
`(3)/((s^2+9)^2).`