Question

Given f of x is equal to the quantity x plus 4 end quantity divided by the quantity x squared minus 3x minus 28 end quantity, which of the following is true? f(x) is positive for all x > –4 f(x) is negative for all x > –4 f(x) is positive for all x < 7 f(x) is negative for all x < 7

Answer 1

The function
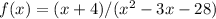`f(x) = (x + 4) / (x^2 - 3x - 28)` changes sign depending on the value of x; it is not consistently positive or negative over the intervals provided in the options (-4 and 7). Therefore, all the given options are incorrect.

Step-by-step explanation:

The function given is
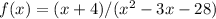`f(x) = (x + 4) / (x^2 - 3x - 28)`. To determine where the function is positive or negative, we must first factor the denominator and find the roots of the equation x2 - 3x - 28 = 0, which factor to (x - 7)(x + 4). Therefore, the roots of the denominator are x = 7 and x = -4, which divide the real number line into three intervals: x < -4, -4 < x < 7, and x > 7. Examining the sign of the function in each interval:

• For x > -4, since the numerator (x + 4) is positive and the denominator changes sign at x = 7, f(x) is positive until x reaches 7 and then becomes negative for x > 7.
• For x < 7, since the numerator (x + 4) changes sign at x = -4, f(x) is negative until x reaches -4 and then becomes positive for -4 < x < 7.

Hence, none of the options provided are correct as the function does not maintain a consistent sign over the intervals mentioned in the options. Specifically, f(x) is not positive for all x > -4 nor is it negative for all x > -4. Similarly, it is not positive for all x < 7 nor negative for all x < 7.

Answer 2

The function f(x) = (x + 4) / (x² - 3x - 28) is positive for all x < -4 and negative for all -4 < x < 7. It is positive again for x > 7. The signs are determined by factoring the denominator and analyzing intervals between the zeros.

Step-by-step explanation:

The question involves analyzing the sign of a rational function f(x) = (x + 4) / (x² - 3x - 28). To determine where the function is positive or negative, we should first factor the quadratic denominator and find the zeros of the function.

The denominator factors to (x - 7)(x + 4). The zeros of the denominator, which are also the vertical asymptotes of the function, are x = 7 and x = -4. Since the numerator is x + 4, it will be zero when x = -4. The sign of the function will change at these zeros.

To analyze the sign of the function:

• For x > 7, both the numerator and denominator are positive, hence the function is positive.
• Between -4 and 7, the numerator is positive, but the denominator is negative, so the function is negative.
• For x < -4, both the numerator and denominator are negative, which results in a positive function.

Therefore, we can conclude that f(x) is positive for all x < -4 and f(x) is negative for all x > -4 and x < 7.