Question

a 3.5 mm thick sheet is rolled using a two high rolling mill to reduce the thickness under plane strain condition. both rolls have a diameter of 500 mm and are rotating at 200 rpm. the coefficient of friction at the sheet and roll interface is 0.08, and the elastic deflection of the rolls is negligible. if the mean flow strength of the sheet material is 400 mpa, then the minimum possible thickness (in mm) of sheet that can be produced in a single pass is _____

Answer 1

The minimum possible thickness of the sheet that can be produced in a single pass under the given conditions is approximately 2.75 mm.

In the process of rolling under plane strain conditions using a two-high rolling mill, various factors influence the minimum possible thickness of the sheet that can be produced in a single pass. The key parameters include the initial thickness of the sheet
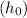`(\(h_0\))`, the diameter of the rolls (D), the rotational speed of the rolls (N), the coefficient of friction at the sheet-roll interface
`(\(\mu\))`, and the mean flow strength of the sheet material
`(\(\sigma\))`.

The formula for the minimum possible thickness
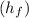`(\(h_f\))` in a single pass under plane strain conditions is given by:

`\[ h_f = h_0 * \left(1 - \left((R * \mu * N)/(\sigma)\right)^(1/2)\right) \]`

where R is the roll radius.

Given the initial thickness
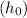`(\(h_0\))` as 3.5 mm, roll diameter (D) as 500 mm (roll radius (R) is 250 mm), rotational speed (N) as 200 rpm, coefficient of friction
`(\(\mu\))` as 0.08, and mean flow strength
`(\(\sigma\))` as 400 MPa, we can substitute these values into the formula to calculate the minimum possible thickness
`(\(h_f\))`.

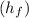After substituting the values, we find that the minimum possible thickness of the sheet that can be produced in a single pass is approximately 2.75 mm.