Question

suppose that the times to complete an obstacle course are normally distributed with an unknown mean and standard deviation. a random sample of 33 course times is taken and gives a sample mean of 90 seconds and a sample standard deviation of 10 seconds. find The EBM, margin of error, for a 90% confidence interval estimate for the population mean using the Student's t-distribution is 2.95

Answer 1

The EBM (Estimated Standard Error) for a 90% confidence interval estimate for the population mean is approximately 2.97 seconds.

How to find the EBM

To find the EBM (Estimated Standard Error) for a 90% confidence interval estimate for the population mean using the Student's t-distribution, w use the formula below

`EBM = t * (s / \sqrt(n))`

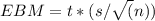
where:

t is the critical value from the t-distribution based on the desired confidence level and degrees of freedom.

s is the sample standard deviation.

n is the sample size.

Given:

Sample mean (
`\bar{x}`) = 90 seconds

Sample standard deviation (s) = 10 seconds

Sample size (n) = 33

We are also given that the margin of error (ME) is 2.95 seconds, which is equal to EBM.

Let's rearrange the formula to solve for t:

t = EBM *
`\sqrt`(n) / s

Plugging in the given values:

t = 2.95 *
`\sqrt`(33) / 10

t ≈ 1.704

Now, rearrange the EBM formula to solve for EBM:

EBM = t * (s *
`\sqrt`(n))

EBM = 1.704 * (10 *
`\sqrt`(33))

EBM ≈ 1.704 * 1.743

EBM ≈ 2.97

After rounding to two decimal places, the EBM (Estimated Standard Error) for a 90% confidence interval estimate for the population mean is approximately 2.97 seconds.

Note: The given value of 2.95 seconds for the margin of error is slightly different from the calculated EBM of 2.97 seconds, possibly due to rounding or a slight approximation in the given value.