Question

Three common methods of solving quadratic equations are graphing, factoring and using the

quadratic formula. Choose 2 methods to solve the equation below.
If you choose factoring or the quadratic formula, you must SHOW ALL WORK.
If you choose graphing you must SKETCH the graph and label the solutions on the graph.
2x² + x - 150
PLS DO FACTORING AND USING THE QUADRATIC FORMULA !!!!

Answer 1

The solution of the quadratic equation using the factoring method and the quadratic formula is; x = 2.5 and x = -3

The steps for the factoring and quadratic formula methods used for solving the quadratic equation can be presented as follows;

The quadratic function can be presented as follows;

2·x² + x - 15 = 0

The above equation can be solved using the factoring method to get;

Factoring the above equation, we get;

2·x² + 6·x - 5·x - 15 = 0

2·x·(x + 3) - 5·(x + 3) = 0

2·x·(x + 3) - 5·(x + 3) = (2·x - 5)·(x + 3)

(2·x - 5)·(x + 3) = 0

Therefore; 2·x - 5 = 0 or x + 3 = 0

x = 5/2 and x = -3

5/2 = 2.5

x = 2.5 and x = -3

The equation 2·x² + x - 15 = 0 can be solved using the quadratic formula as follows;

The quadratic formula for the quadratic equation of the form;

a·x² + b·x + c = 0 is;
`x = (-b \pm√(b^2 - 4\cdot a \cdot c) )/(2\cdot a)`

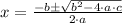
Comparing the specified quadratic equation with the equation for the quadratic formula, we get;

x = (-1 ± √(1² - 4 × 2 × (-15)))/(2 × 2)

x = (-1 ± 11))/(4)

x = 10/4 and x = -12/4

x = 2.5 and x = -3