Question

Yoo can someone help me please, im so lost


thank u sm if u do

Answer 1

Explanation:

3√2 = a/b

where b ≠ 0

√2 = a/3b

1.4 = a / 3b

for any possible value of a and b we cannot satisfy this equation i.e. we cannot prove that RHS = LHS

thus, the assumption is wrong

therefore, 3√2 is irrational

Answer 2

rational, irrational, and irrational

Explanation:

The image you've uploaded contains a mathematics problem involving proof by contradiction for the irrationality of the number 3√2. The problem statement is incomplete as it requires choices to be filled in to complete the proof.

`\hrulefill`

The proof:

Assume that 3√2 is rational. This means that it can be expressed as a ratio of two integers, where 'a' and 'b' have no common factors (other than 1), and b ≠ 0.

`\Longrightarrow 3 \sqrt2=(a)/(b)`

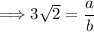
Now, isolate √2 by dividing both sides by 3:

`\Longrightarrow \sqrt2=(a)/(3b)`

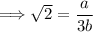
If 'a' and 'b' are integers, then a/3b is also rational, because the ratio of two integers is rational. Next, square both sides to eliminate the square root:

`\Longrightarrow (\sqrt2)^2=((a)/(3b))^2\\\\\\\\\Longrightarrow 2=(a^2)/(3^2b^2)\\\\\\\\\Longrightarrow 2=(a^2)/(9b^2)`

Now multiply both sides by 9b² to solve for a²:

`\Longrightarrow a^2 = 2(9b^2)\\\\\\\\\Longrightarrow a^2 = 18b^2`

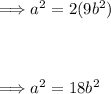
This implies that a² is an even number since it's equal to 18b², which is clearly a multiple of 2. If a² is even, then 'a' must also be even (only the square of an even number is even).

Let's say a = 2k where 'k' is an integer. Then:

`\Longrightarrow (2k)^2 = 18b^2\\\\\\\\\Longrightarrow 4k^2 = 18b^2\\\\\\\\\Longrightarrow 2k^2 = 9b^2`

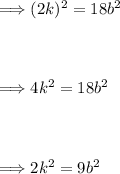
This equation implies that 9b² is even, which in turn implies that b² (and hence b) must be even. But this contradicts our initial assumption that 'a' and 'b' have no common factors other than 1 (since both are now even, they are both divisible by 2).

`\hrulefill`

Addressing the image:

To complete the proof, the following choices should be made:

• Right side of the equation is: "rational" (because 'a' and 'b' are integers and the quotient of two integers is rational).

• The left side of the equation is "irrational" (because the square root of 2 is known to be irrational and multiplying an irrational number by a rational number results in an irrational number).

• Therefore, the number 3√2 is "irrational".