Part A: The complex conjugate is
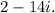
Part B: The final answer in standard form (a + bi) is
![\[ -(1)/(20) - (23)/(20)i \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bns4tysammt7afbytm558ozm2tbjvj0pef.png)
How did we get the values?
Given complex numbers:
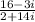
Part A: Complex Conjugate of the Denominator
The complex conjugate of a complex number
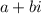 is
is
 For the given denominator
For the given denominator
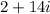 , the complex conjugate is
, the complex conjugate is
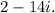
Part B: Quotient in Standard Form (a + bi)
To find the quotient, we need to multiply the given expression by the conjugate of the denominator over itself. This is done to eliminate the imaginary part from the denominator.
![\[ (16 - 3i)/(2 + 14i) \cdot (2 - 14i)/(2 - 14i) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tzpxstb429ovd1jvrfg0q1evk81fx4tnj1.png)
Now, multiply the numerators and denominators:
Numerator:
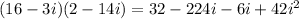
Simplify:
 (because
(because
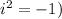
Combine like terms:

Denominator:
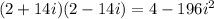
Simplify:
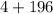 (because
(because
 )
)
Combine like terms:
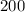
Now, the quotient is:
![\[ (-10 - 230i)/(200) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2jsqeomlr55i9mkg88b750k8ogt92yn5wq.png)
Simplify the fraction by dividing both the real and imaginary parts by 10:
![\[ (-1 - 23i)/(20) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/shsl0uvh7qm4v31t6wkpifxl0e87gvv50p.png)
So, the final answer in standard form (a + bi) is:
![\[ -(1)/(20) - (23)/(20)i \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bns4tysammt7afbytm558ozm2tbjvj0pef.png)