The moment of inertia of a rectangular beam with a base of 4 inches and a height of 3 inches is
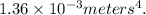
The moment of inertia of a rectangular beam can be calculated using the formula
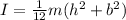, where I is the moment of inertia, m is the mass of the beam, and h and b are the height and base of the beam respectively.
In this case, the base of the beam is 4 inches and the height is 3 inches.
To calculate the moment of inertia, we need to convert the measurements to meters.
4 inches is equal to 0.1016 meters and 3 inches is equal to 0.0762 meters.
Assuming the beam has a uniform mass, we can use the formula I = $rac{1}{12} m (h^2 + b^2)$ = $rac{1}{12} (0.1016)(0.0762^2 + 0.1016^2)$ = $rac{1}{12} (0.1016)(0.00581984 + 0.01031216)$ = $rac{1}{12} (0.1016)(0.016132)$ = 0.001357629568 meters^4 or 1.36 x 10^-3 meters^4.