Question

5. A man pulls a 50.0 kg box up a ramp inclined at 12° with the horizontal. If the box

starts from rest and the man pulls with a 250 N force, what is the acceleration of the box
up the ramp
a) if it is frictionless.
b) if it has a coefficient of friction µ = 0.20.

Answer 1

a) 3.0 m/s²

b) 1.0 m/s²

Step-by-step explanation:

There are four forces acting on the box:

Weight force mg pulling down,

Normal force N pushing normal to the incline,

Friction force Nμ pushing parallel down the incline,

and applied force P pushing parallel up the incline.

Sum of forces in the normal direction:

∑F = ma

N − mg cos θ = 0

N = mg cos θ

Sum of forces in the parallel direction:

∑F = ma

P − Nμ − mg sin θ = ma

P − mg cos θ μ − mg sin θ = ma

P − mg (μ cos θ + sin θ) = ma

a = P/m − g (μ cos θ + sin θ)

a) If μ = 0:

a = (250 N) / (50.0 kg) − (9.8 m/s²) (0 + sin 12°)

a = 2.962 m/s²

b) If μ = 0.20:

a = (250 N) / (50.0 kg) − (9.8 m/s²) (0.20 cos 12° + sin 12°)

a = 1.045 m/s²

Rounded to two significant figures, the accelerations are 3.0 m/s² and 1.0 m/s².

Answer 2

(a) 2.96 m/s²

(b) 1.05 m/s²

Step-by-step explanation:

To find the acceleration of the box in both scenarios, we need to consider the forces acting on it and use Newton's second law of motion, ΣF = ma, where 'ΣF' is the net force, 'm' is the mass, and 'a' is the acceleration.

I have attached an image that was used as reference for the below explanation.

Given:

• F = 250 N
• m = 50.0 kg
• μ = 0.20
• θ = 12°

`\hrulefill`

a) Frictionless Ramp
`\hrulefill`

To find the acceleration of the box when the ramp is frictionless, we will use the sum of forces acting horizontally on the box. Let's add up forces:

`\sum \vec F_x: \vec F + \vec w \cos(270\textdegree - \theta)=m \vec a`

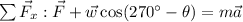
Solving the above for 'a' we get:

`\Longrightarrow \vec F + \vec w \cos(270\textdegree - \theta)=m \vec a\\\\\\\\ \Longrightarrow \vec a= (\vec F + \vec w \cos(270\textdegree - \theta))/(m)`

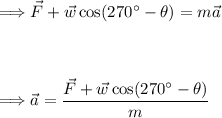
The weight 'w' is equal to the boxes mass times the acceleration from gravity, substitute this in:

`\Longrightarrow \vec a= (\vec F + mg \cos(270\textdegree - \theta))/(m)`

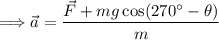
Now we can plug in our know values and use a calculator to simplify:

`\Longrightarrow \vec a= \frac{250 \text{ N} + (50.0 \text{ kg})(9.8 \text{ m/s$^2$}) \cos(270\textdegree - 12 \textdegree)}{50.0 \text{ kg}}\\\\\\\\\therefore \vec a \approx \boxed{2.96 \text{ m/s$^2$}}`

Thus, the acceleration of the box on the frictionless ramp is approximately 2.96 m/s².

`\hrulefill`

b) Ramp with Friction
`\hrulefill`

To find the acceleration of the box when the ramp has friction, we will use the sum of forces acting horizontally and vertically on the box. Let's add up forces horizontally first:

`\sum \vec F_x: \vec F- \vec f_k + \vec w \cos(270\textdegree - \theta)=m \vec a`

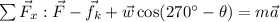
Solving the above for 'a' we get:

`\Longrightarrow \vec F- \vec f_k + \vec w \cos(270\textdegree - \theta)=m \vec a\\\\\\\\\Longrightarrow \vec a=(\vec F- \vec f_k + \vec w \cos(270\textdegree - \theta))/(m)\\\\\\\\\Longrightarrow \vec a=(\vec F- \mu \vec n + mg \cos(270\textdegree - \theta))/(m) \ \Big[\because \vec f_k = \mu \vec n\Big]`

We do not know the normal force, we will find this using the vertical components. Summing these up:

`\sum \vec F_x: \vec n + \vec w \sin(270\textdegree - \theta)=0`

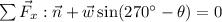
Solving for 'n':

`\Longrightarrow \vec n + \vec w \sin(270\textdegree - \theta)=0\\\\\\\\\Longrightarrow \vec n =- \vec w \sin(270\textdegree - \theta)\\\\\\\\\Longrightarrow \vec n =- mg \sin(270\textdegree - \theta)`

Plug in what we know to find the normal force:

`\Longrightarrow \vec n =- (50.0 \text{ kg})(9.8 \text{ m/s$^2$}) \sin(270\textdegree - 12 \textdegree)\\\\\\\\\therefore n \approx 479.29 \text{ N}`

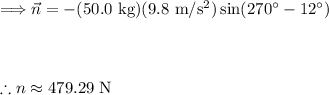
Using the normal force above and the sum of the horizontal forces, we can find the acceleration of the box:

`\Longrightarrow \vec a=\frac{250 \text{ N}- (0.20)(479.29 \text{ N})+ (50.0 \text{ kg})(9.8 \text{ m/s$^2$}) \cos(270\textdegree - 12 \textdegree)}{50.0 \text{ kg}}\\\\\\\\\therefore \vec a \approx \boxed{1.05 \text{ m/s$^2$}}`

Thus, the acceleration of the box on the ramp is approximately 1.05 m/s².