Question

A science test, which is worth 100 points, consists of 24 questions. Each question is worth either 3 points or 5 points. If x is the number of 3-point questions and y is the number of 5-point questions, the system shown represents this situation.

x + y = 24
3x + 5y = 100

What does the solution of this system indicate about the questions on the test?

The test contains 4 three-point questions and 20 five-point questions.
The test contains 10 three-point questions and 14 five-point questions.
The test contains 14 three-point questions and 10 five-point questions.
The test contains 20 three-point questions and 8 five-point questions.

Answer 1

The test contains 10 three-point questions and 14 five-point questions.

Explanation:

To determine the solution to the system, let's solve it:

Given system of equations:

`\sf \begin{cases} x + y = 24 \\ 3x + 5y = 100 \end{cases}`

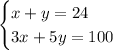
We can use either substitution or elimination to solve this system. I'll use substitution:

From the first equation, we can express
`\sf x` in terms of
`\sf y`:

`\sf x = 24 - y`

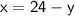
Now, substitute this expression for
`\sf x` into the second equation:

`\sf 3(24 - y) + 5y = 100`

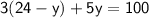
Distribute and combine like terms:

`\sf 72 - 3y + 5y = 100`

`\sf 2y = 28`

`\sf y = 14`

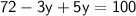
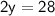
Now that we have the value for
`\sf y`, substitute it back into the equation
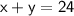`\sf x + y = 24` to find
`\sf x`:

`\sf x + 14 = 24`

`\sf x = 10`

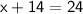
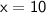
So, the solution to the system is
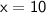`\sf x = 10` and
`\sf y = 14`. This means there are 10 three-point questions and 14 five-point questions.

So, the answer is:

The test contains 10 three-point questions and 14 five-point questions.