Question

The proportional relationship between two variables, x and y, is represented by x, equals, start fraction, 7, divided by, 2, end fraction, yx= 2 7 ​ y. What is the constant of proportionality from yy to xx

Answer 1

The constant of proportionality from y to x in the given relationship

`\(x = (7)/(2)y\)` is
`\((2)/(7)\)`. For every unit increase in y, x increases by
`\((2)/(7)\)` units.

Let's break down the calculation step by step for the given proportional relationship:

`\[ x = (7)/(2)y \]`

Step 1: Identify the constant of proportionality

The constant of proportionality is the coefficient of y, which is
`\((7)/(2)\).`

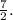
Step 2: Interpret the relationship

This means that for every unit increase in y, x increases by
`\((7)/(2)\)` units, and for every unit decrease in y, x decreases by the same proportion.

Step 3: Solve for y in terms of x

If you want to express y in terms of x, you can rearrange the equation:

`\[ x = (7)/(2)y \]`

Multiply both sides by
`\((2)/(7)\)` to isolate y:

`\[ y = (2)/(7)x \]`e

Now, you can see that the constant of proportionality from y to x is

`\((2)/(7)\).`

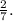
Summary:

The constant of proportionality from y to x is
`\((7)/(2)\)`, indicating the relationship between x and y. If you express y in terms of x, it becomes
`\((2)/(7)x\)`, demonstrating the consistent proportionality between the two variables.

Que. The proportional relationship between two variables, x and y, is represented by x= (7)/(2)y. What is the constant of proportionality from y to x