Question

A product is sold in stores for 40 % more than the wholesale price from the manufacturer. The manufacturer makes 100 % profit on the product’s manufacturing cost. What must the manufacturing cost be if the product sells in stores for $1.75?

Answer 1

The manufacturing cost must be approximately $0.625 for the product to sell in stores for $1.75.

How did we get the value?

Let's denote the manufacturing cost as
`\(C\)`. The manufacturer makes a 100% profit on this cost, so the selling price to the store is
`\(C + 100\% \cdot C = 2C\).`

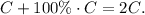
The product is sold in stores for 40% more than the wholesale price, so the selling price in stores is
`\(2C + 40\% \cdot 2C = 2C + 0.4 \cdot 2C \\= 2C + 0.8C \\= 2.8C\).`

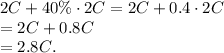
We are given that the product sells in stores for $1.75, so we can set up the equation:

`\[2.8C = 1.75\]`

Now, solve for
`\(C\)`:

`\[C = (1.75)/(2.8)\]`

`\[C \approx 0.625\]`

So, the manufacturing cost must be approximately $0.625 for the product to sell in stores for $1.75.