The height of the tree is approximately 1.56 meters.
To find the height of the tree, we can set up a proportion using the similar triangles formed by Scarlett and the tree.
Let H be the height of the tree.
The proportion can be set up as follows:
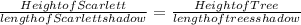
Substitute the given values:
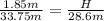
Now, solve for H:
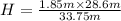
Calculate this value:
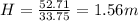
So, the height of the tree is approximately 1.56 meters.