Final answer:
The derivative of the function f(x) = 5x is f'(x) = 5. The derivative of a constant multiplied by \( x \) is the constant itself. In this case, the derivative of
 spect to \( x \) is 5.
spect to \( x \) is 5.
Step-by-step explanation:
The question asks for the derivative of the function f(x) = 5x. To find the derivative, we can use the power rule, which states that the derivative of x^n is nx^(n-1), where n is a constant. In this case, the constant is 5. So, the derivative of f(x) = 5x is f'(x) = 5.
The derivative of a function
 ect to \( x \), is denoted as
ect to \( x \), is denoted as

 the rate at which the function is changing with respect to
the rate at which the function is changing with respect to
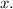
For the function
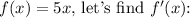
![\[ f'(x) = (d)/(dx)(5x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/s7zjjoo1bqybkhcrvarr1krf47rb16i2nc.png)
The derivative of
 spect to
spect to
 ply the coefficient of
ply the coefficient of
 is 5.
is 5.
So,
