Question

Carol Danvers swims across the Atlantic Ocean with a velocity of 25.0 km/hr at 290°. If there's a current moving against her at 3.2 km/hr at 32°, what will her actual velocity be?

A) 28.2 km/hr at 258°
B) 21.8 km/hr at 322°
C) 28.2 km/hr at 32°
D) 21.8 km/hr at 148°

Answer 1

C) 28.2 km/hr at 32°

To find the resultant velocity, vector addition is used, combining Carol Danvers' swim velocity with the current. After converting polar coordinates to Cartesian components, the resultant velocity is approximately
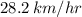`\(28.2 \, km/hr\)` at an angle of
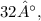`\(32°\),` matching option C.

Step-by-step explanation

To determine Carol Danvers' actual velocity, we can use vector addition to combine her swimming velocity with the velocity of the current. The given velocities are in polar coordinates, and we need to convert them into their respective Cartesian components.

Let
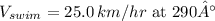`\(V_(swim) = 25.0 \, km/hr\) at \(290°\)` be the velocity of Carol Danvers, and
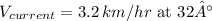`\(V_(current) = 3.2 \, km/hr\) at \(32°\)`be the velocity of the current.

The horizontal component of the swim velocity
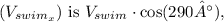`(\(V_(swim_x)\)) is \(V_(swim) \cdot \cos(290°)\),` and the vertical component
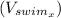`(\(V_(swim_x)\))`is
`\(V_(swim) \cdot \cos(290°)\),`. Similarly, for the current velocity,
`\(V_(current_x) = V_(current) \cdot \cos(32°)\) and \(V_(current_y) = V_(current) \cdot \sin(32°)\).`

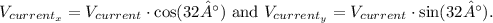
Now, adding the horizontal and vertical components separately, we get the resulting velocity
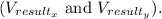`(\(V_(result_x)\) and \(V_(result_y)\)).`The magnitude of the resulting velocity is given by
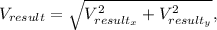`\(V_(result) = \sqrt{V_(result_x)^2 + V_(result_y)^2}\),`and the direction angl
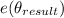`e (\(\theta_(result)\))` is given by
`\(\tan^(-1)\left((V_(result_y))/(V_(result_x))\right)\).`

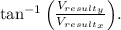
Calculating these values, we find that the actual velocity is approximately
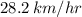`\(28.2 \, km/hr\)` at an angle of
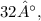`\(32°\),` matching option C. This indicates that Carol Danvers will be swimming with an actual velocity of
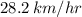`\(28.2 \, km/hr\)`at an angle of
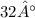`\(32°\)` relative to the eastward direction.