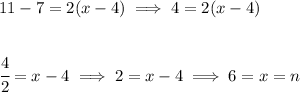Question

Find the rule , solve for n

Answer 1

the assumption here being that the graph is a straight line, so to get the "rule" or just its equation, all we need is two points from it hmmm say let's use (4 , 7) and (8 , 15) from the table

`(\stackrel{x_1}{4}~,~\stackrel{y_1}{7})\qquad (\stackrel{x_2}{8}~,~\stackrel{y_2}{15}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{15}-\stackrel{y1}{7}}}{\underset{run} {\underset{x_2}{8}-\underset{x_1}{4}}}\implies \cfrac{8}{4}\implies 2 \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{7}=\stackrel{m}{2}(x-\stackrel{x_1}{4})`

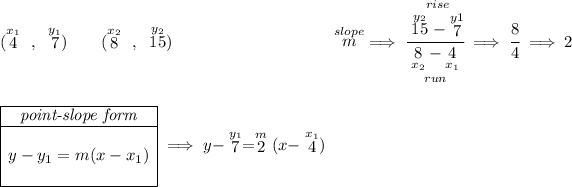
and we can use that as is, so, now, what's "x" when y = 11?

`11-7=2(x-4)\implies 4=2(x-4) \\\\\\ \cfrac{4}{2}=x-4\implies 2=x-4\implies 6=x=n`