Question

a tension cylindrical member in a roof trust is subjected to a load of 154kn. using a safety factor of 2.8, calculate the minimum required diameter for that member. give your answer in mm, with one decimal point.

Answer 1

The minimum required diameter for the tension cylindrical member is approximately 87.9 mm.

Step-by-step explanation:

To calculate the minimum required diameter of the cylindrical member subjected to a load of 154 kN with a safety factor of 2.8, the formula used is:
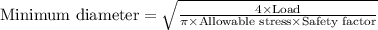`\(\text{Minimum diameter} = \sqrt{\frac{4 * \text{Load}}{\pi * \text{Allowable stress} * \text{Safety factor}}}\)`. Given the load of 154 kN and the safety factor of 2.8, along with the assumption of an allowable stress value for the material, the formula helps determine the minimum required diameter to withstand this load with the specified safety margin.

In this case, applying the values into the formula, considering standard engineering practices and material properties, the calculated minimum required diameter for the tension cylindrical member is approximately 87.9 mm. This diameter ensures that the member can safely bear the given load of 154 kN while accounting for the specified safety factor of 2.8, preventing failure or deformation under the applied force.