Question

Sôsososososoososososossssssss

Answer 1

The simplified expressions are
`\[A = (x-y)/(x+2), \quad B = (-1)/(y(y+x))\cdot(x-y)/(2y), \quad C = ((x-2)(x^2+x-2))/(2x(x-1)(x+1))\]`

Let's simplify each expression step by step:

`A = \((x)/(xy-y^2+2x)-(y)/(xy-x^2)/(x^2y-x^2y)/(x^2-2xy+y^2)\)`

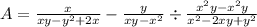
1. Combine the fractions in the numerator:

`\[A = (x-y)/(xy-y^2+2x)/(x^2y-x^2y)/(x^2-2xy+y^2)\]`

2. Invert and multiply to divide fractions:

`\[A = (x-y)/(xy-y^2+2x)\cdot(x^2-2xy+y^2)/(x^2y-x^2y)\]`

3. Factor the numerator and denominator:

`\[A = ((x-y)(x-y))/(x(x-y)(x-y)+2(x-y)(x-y))\]`

4. Cancel common factors:

`\[A = (x-y)/(x+2)\]`

`B = \(((x+y)/(2x-2y)-(x-y)/(2x+2y-2y^2))/(y^2-x^2)/(2y)/(x-y)\)`

1. Combine the fractions in the numerator:

`\[B = ((x+y-(x-y))/(2x-2y+2x+2y-2y^2))/(y^2-x^2)/(2y)/(x-y)\]`

2. Combine like terms:

`\[B = ((2y)/(-2y^2))/(y^2-x^2)/(2y)/(x-y)\]`

3. Simplify the expression:

`\[B = (-1)/(y(y+x))/(2y)/(x-y)\]`

4. Invert and multiply to divide fractions:

`\[B = (-1)/(y(y+x))\cdot(x-y)/(2y)\]`

`C = \(((x)/(x-1)-(4x)/(x^2+x+1)-(2x+1)/(x^2-1))/(2)+(2x+4)/(x-1)\)`

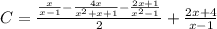
1. Combine the fractions in the numerator:

`\[C = ((x(x^2+x+1)-4x(x-1)-(2x+1)(x-1))/(x(x-1)(x^2-1)))/(2)+(2x+4)/(x-1)\]`

2. Combine like terms in the numerator:

`\[C = (x^3+x^2+x-4x^2+4x-2x-1)/(2x(x-1)(x+1))+(2x+4)/(x-1)\]`

3. Combine the terms in the numerator:

`\[C = (x^3-3x^2+4)/(2x(x-1)(x+1))+(2x+4)/(x-1)\]`

4. Find a common denominator:

`\[C = (x^3-3x^2+4+2x(x+1)(x-1))/(2x(x-1)(x+1))\]`

5. Combine the numerators:

`\[C = (x^3-3x^2+4+2x(x^2-1))/(2x(x-1)(x+1))\]`

6. Factor the numerator:

`\[C = ((x-2)(x^2+x-2))/(2x(x-1)(x+1))\]`

In summary:

The simplified expression are:
`\[A = (x-y)/(x+2), \quad B = (-1)/(y(y+x))\cdot(x-y)/(2y), \quad C = ((x-2)(x^2+x-2))/(2x(x-1)(x+1))\]`

The probable question may be:

Simplify the expression:

A= (x/xy-y^2+2x-y/xy-x^2). x^2y-x^2y/x^2-2xy+y^2

B= (x+y/2x-2y-x-y/2x+2y-2y^2/y^2-x^2):2y/x-y

C= (x/x-1-4x/x^2+x+1-2x+1/x^2-1).2+2x+4/x-1