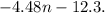1.
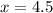 hours.
hours.
4.
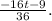
5.
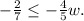
6.
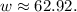
7.

8.
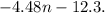
How did we get the values?
Let's go through each question one by one:
Question 1:
The correct equation is:
![\[35 + 60x = 305\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1ougjzmzi4u859yhmctzczjzpimialrlmb.png)
where
 is the number of hours worked.
is the number of hours worked.
Solving for
 :
:
![\[60x = 305 - 35\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/u1wwunmx1mvttyjoo7js8k5k9zryppgat7.png)
![\[60x = 270\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/s4gbf7ctwtzltbs8szj9o19l7k7gldf3es.png)
![\[x = (270)/(60) = 4.5\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cw3etx4f1e5ca7zqcaobfoncy1997zhpty.png)
So, the correct answer is:
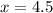 hours.
hours.
Question 4:
Which expression is equivalent to the expression
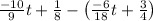 ?
?
Combine like terms:
![\[(-10)/(9)t + (1)/(8) + (6)/(18)t - (3)/(4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lqqnt6lo36ql1nezy4skzdigevnuogzcco.png)
Find a common denominator for the fractions:
![\[(-80t + 9 + 48t - 27)/(72)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ckg2hkaisyn3lz146v25hcjaktoqf23ulw.png)
Combine the numerators:
![\[(-32t - 18)/(72)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dwkqw08kr4jsm67bwgdg3uau079xmfverj.png)
Simplify by dividing both numerator and denominator by their greatest common factor (6):
![\[(-16t - 9)/(36)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/i7gq4tnwkos5m7q81sbb2lisn3mepk0ftf.png)
So, the correct answer is:
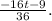
Question 5:
Write an inequality for the statement:
 is at most the product of a number and
is at most the product of a number and
 .
.
The correct inequality is:
![\[-(2)/(7) \leq -(4)/(5)w\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/o8tp284qm9tnu4qwpit8lr857gnwrvhg1u.png)
So, the correct answer is:
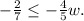
Question 6:
Solve the equation for
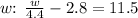
First, add 2.8 to both sides:
![\[(w)/(4.4) = 14.3\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/m8inu25fvc8iongzdnrue28o54j7pq1mky.png)
Then, multiply both sides by 4.4:
![\[w = 4.4 * 14.3\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nu100onwh8fhe20w4f8r4cujenhc69avyz.png)
Calculating this gives:
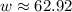
So, the correct answer is:
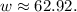
Question 7:
Which equation represents the written description? "Seven times the difference between 35.8 and a number is equal to 53.4".
The correct equation is:
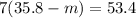
So, the correct answer is:

Question 8:
Subtract the expressions:
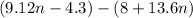
Combine like terms:
![\[9.12n - 4.3 - 8 - 13.6n\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ulpegb7w87klsjm826f3pmsvdgjcvtv0li.png)
Combine the
 terms:
terms:
![\[-4.48n - 12.3\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tdbf12xvthm8938mhja9mn7hg0jr4ar10r.png)
So, the correct answer is: