By algebra properties and trigonometric formulae, the trigonometric equation
 is equivalent to
is equivalent to
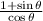 .
.
How to prove a trigonometric equivalence
In this question we find the case of a trigonometric equivalence that must be proved. This can be done by using algebra properties and trigonometric formulae. The procedure consists in starting on one side of the equivalence and modifying it until the expression of the other side is found.
First, write one side of the trigonometric equivalence:

Second, use algebra properties and trigonometric equivalence to expand and simplify the resulting expression:

![([(1 + \sin \theta) + \cos \theta]\cdot [(1 + \sin \theta) - \cos \theta])/([(1 -\sin \theta)+\cos \theta] \cdot [(1 + \sin \theta) - \cos \theta])](https://img.qammunity.org/2024/formulas/mathematics/high-school/8t7dg0iokzmzo3lspudvilw7dy0md8vdap.png)
![((1 + \sin \theta)^2- \cos^2 \theta)/([1 - (\sin \theta - \cos \theta)]\cdot [1 + (\sin \theta - \cos \theta)])](https://img.qammunity.org/2024/formulas/mathematics/high-school/2oybfcdc3imdd9u918jpdhyzetno1lszzw.png)

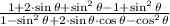
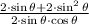
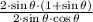
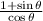
By algebra and trigonometry, the trigonometric equation
 is equivalent to the trigonometric equation
is equivalent to the trigonometric equation
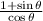 .
.