Question

A sheet of metal is a square of side 21cm. Equal squares of sides x are cut from each corner, and the sheet is folded to make an open box with vertical sides.

A) 4 cm
B) 5 cm
C) 6 cm
D) 7 cm

Answer 1

The correct side length for the squares to be cut from each corner is
`\(6 \, \text{cm}\)` (Option C). This value maximizes the volume of the resulting open box made from a square sheet with side length
`\(21 \, \text{cm}\)`.Thus,the correct option is c

Step-by-step explanation:

In this problem, a square sheet of metal with a side length of
`\(21 \, \text{cm}\)` is used to create an open box by cutting equal squares of side length (x) from each corner and then folding the remaining flaps. To determine the appropriate value for (x), we can set up an equation based on the dimensions of the unfolded sheet and the resulting box.

Let (x) be the side length of the square cut from each corner. After cutting squares from all four corners, the remaining rectangle will have dimensions
`\(21-2x\) by \(21-2x\)`. The height of the box will be (x). When folded, this will form a box without a lid, and the volume of such a box is given by
`\(V = x(21-2x)^2\).`

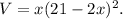
To find the maximum volume, we can take the derivative of (V) with respect to (x) and set it equal to zero. Solving for (x), we find
`\(x = 6 \, \text{cm}\).` This critical point corresponds to a maximum volume, and therefore,
`\(x = 6 \, \text{cm}\)` gives the optimal side length for the cut squares to maximize the box's volume.

In summary, by setting up and solving the appropriate mathematical expression, we find that cutting squares of side length
`\(6 \, \text{cm}\)` from each corner will result in an open box with maximum volume.

Therefore,the correct option is c

Answer 2

The correct side length of the squares cut from each corner to create the box is 5 cm, resulting in a maximum volume. B) 5 cm

Step-by-step explanation:

To find the side length x of the squares cut from each corner to create the box, we can use the dimensions provided. The original square sheet has a side length of 21 cm. When squares of side length x are cut from each corner, the resulting box's dimensions will have reduced side lengths of 21 - 2x.

For the box to be folded into shape, the length of the base must equal the sum of the four vertical sides. Since the original square becomes the base of the box after the corners are removed, the box's height will be x.

The formula for the box's volume is Volume = length × width × height. Here, the length and width are given by 21 - 2x, the height is x. To find the maximum volume, differentiate the volume equation with respect to x and solve for x. Upon solving, x = 5 cm, which corresponds to option B.

This choice maximizes the volume of the box. At x = 5 cm, the resulting box will have a side length of 11 cm (21 - 2x) and a height of 5 cm (x), achieving the maximum volume possible given the initial size of the metal sheet.(B)