Question

A function, f(x), passes through the point (0,2). Another function is represented by the equation g(x)=x^2−2x−3. What is the y-intercept of g(x) and which function has the greater y-intercept

Answer 1

• The y-intercept of function f(x) is 2.

• The y-intercept of function g(x) is -3.

Therefore, we conclude that function f(x) has a greater y-intercept.

Explanation:

The y-intercept of any function can be determined by checking the value of y at x = 0.

Important Tip

• A point where the graph meets the y-axis — y-intercept.

Determining the y-intercept of the function f(x)

Given the function f(x) passes through the point (0,2).

It means at x = 0, the value of y = 2

Thus, the y-intercept of function f(x) is 2.

Determining the y-intercept of the function g(x)

Given the function g(x)

`g\left(x\right)=x^2-2x-3`

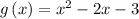
substitute x = 0 in the function equation

`g\left(0\right)=\left(0\right)^2-2\left(0\right)-3`

`g\left(0\right)=0-0-3`

`g\left(0\right)=-3`

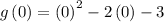
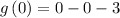
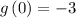
It means at x = 0, the value of y = -3

Thus, the y-intercept of function g(x) is -3.

Conclusion:

• The y-intercept of function f(x) is 2.

• The y-intercept of function g(x) is -3.

As 2 > -3

Therefore, we conclude that function f(x) has a greater y-intercept.