Answer:
See Below
Explanation:
Statements: Reasons:
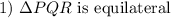 Given
Given
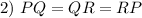 Definition of Equilateral
Definition of Equilateral
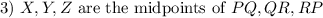 Given
Given
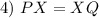 Definition of Midpoint
Definition of Midpoint
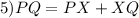 Segment Addition
Segment Addition
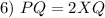 Substitution
Substitution
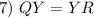 Definition of Midpoint
Definition of Midpoint
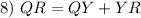 Segment Addition
Segment Addition
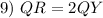 Substitution
Substitution
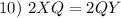 Substitution
Substitution
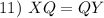 Division Property of Equality
Division Property of Equality
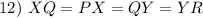 Transitive Property
Transitive Property
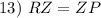 Definition of Midpoint
Definition of Midpoint
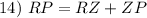 Segment Addition
Segment Addition
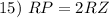 Substitution
Substitution
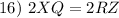 Substitution
Substitution
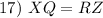 Substitution
Substitution
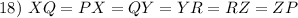 Transitive Property
Transitive Property
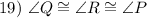 Definition of Equilateral
Definition of Equilateral
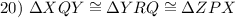 SAS Congruence
SAS Congruence
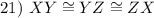 CPCTC
CPCTC
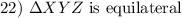 Equilateral Triangle Theorem
Equilateral Triangle Theorem