Question

D/dx √^3 − 6 help me

Answer 1

The derivative of √
`(x^3 - 6)` is calculated using the chain rule and simplifies to √
`3x^4 / 2√(x^3 - 6).`

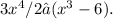
The expression D/dx √
`(x^3 - 6)` asks us to find the derivative with respect to x of the square root of
`(x^3 - 6)`

This is a calculus problem that involves using the chain rule for differentiation.

To evaluate this, we'll take the derivative of the outer function, which is the square root, and multiply it by the derivative of the inner function, which is
`(x^3 - 6)`

Let's break down the steps:

The outer function is √(u), and its derivative is ½u^(-½), by the power rule.

The inner function u is
`(x^3 - 6)` , and its derivative is
`3x^2`, by the power rule.

Applying the chain rule, we multiply the derivatives of the outer and inner functions:
`1/2(x^3 - 6)^((-1/2)) * 3x^2.`

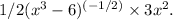
Simplify to get the final answer: √
`(x^3 - 6)` 's derivative is ½ ×
`3x^2` / √
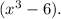`(x^3 - 6).`which simplifies to √
`3x^4` / 2√
`(x^3 - 6).`

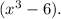
The probable question may be:

Evaluate the expression D/dx √(x^3 - 6)