Question

As you can see in the following diagram, b= 17.4, c=19.6, and ZA 30. Use the Law of Cosines in the form a²b2+²-2bc cos (A) to find

the length a. Round your answer to the nearest hundredth.
C
30°
O a=3.25
O a = 9.81
a = 33.12
17.4
O a = 9.02
19.6
a
B

Answer 1

The correct answer is option c. 9.02 units.

To find the length of side \(a\) in the triangle with angle \(C\) measuring 30 degrees, and sides \(b = 17.4\) and \(c = 19.6\), we use the Law of Cosines:

`\[a^2 = b^2 + c^2 - 2bc \cos(A)\]`

Substitute the given values:

`\[a^2 = 17.4^2 + 19.6^2 - 2(17.4)(19.6) \cos(30^\circ)\]`

`\[a^2 = 302.76 + 384.16 - 2(17.4)(19.6) \cdot (√(3))/(2)\]`

`\[a^2 = 686.92 - 338.64 √(3)\]`

Now, calculate \(a\) by taking the square root:

`\[a = \sqrt{686.92 - 338.64 √(3)}\]`

Rounding to the nearest hundredth,
`\(a \approx 9.02\).`

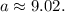
The question probable maybe:

In the triangle shown below, angle C measures 30 degrees, side b is 17.4, and side c is 19.6. Apply the Law of Cosines in the form
`\(a^2 = b^2 + c^2 - 2bc \cos(A)\)` to determine the length of side a. Round your answer to the nearest hundredth.

Given:

- Angle C = 30 degrees

- Side b = 17.4

- Side c = 19.6

Options:

i.
`\(a = 3.25\)`

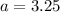
ii.
`\(a = 9.81\)`

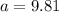
iii.
`\(a = 33.12\)`

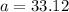
iv.
`\(a = 9.02\)`

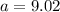
Use the Law of Cosines to find the length of side a and choose the correct option.