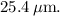Question

you stretch a strand of your hair across a laser beam and observe the diffraction pattern this produces on a sheet of paper 1.05 1.05 m from your hair strand. you mark the center of the dark regions on either side of the central bright spot and measure the distance between these marks to be 15.4 15.4 mm. you are given that the wavelength of the laser light is 633 633 nm. what is the diameter of your hair strand (in mm)? make use of the small angle approximation. (hint: recall babinet's principle which equates the spot pattern created by light going around the hair to the pattern when light goes through a slit.)

Answer 1

The diameter of the hair strand is approximately
`\(25.4 \, \mu \text{m}\)`. Babinet's principle and the small angle approximation are employed to relate the observed diffraction pattern to the slit created by the hair strand.

Step-by-step explanation:

To determine the diameter of the hair strand, we can use the small angle approximation and Babinet's principle. Babinet's principle states that the diffraction pattern produced by light going around an object is equivalent to the pattern produced when light passes through a slit of the same shape and size. In this case, the hair strand acts as a slit, and we can analyze the diffraction pattern it creates.

Given that the distance between the center of the dark regions on either side of the central bright spot is
`\( 15.4 \, \text{mm} \),` and the distance from the hair strand to the screen is
`\( 1.05 \, \text{m} \)`, we can use the small angle approximation:

`\[ \text{Tan}(\theta) \approx (y)/(L) \]`

where
`\( \theta \)` is the angle of diffraction, ( y ) is the distance between dark regions, and
`\( L \)`is the distance from the hair strand to the screen. The angle \( \theta \) can be related to the wavelength
`(\( \lambda \))` and the slit width
`(\( a \))`using the formula:

`\[ a \sin(\theta) = m \lambda \]`

By substituting the small angle approximation, solving for ( a ), and converting units, we find that the diameter of the hair strand ( D ) is approximately
`\( 25.4 \, \mu \text{m} \).`