Question

For a given multiple regression model with three independent variables, the value of the adjusted multiple coefficient of determination is _________ less than R2.

a. Always
b. Sometimes
c. Never
d. Can be greater or less depending on the standard error

Answer 1

The adjusted multiple coefficient of determination can never be greater than R^2. Option c.

Step-by-step explanation:

In a multiple regression model with three independent variables, the adjusted multiple coefficient of determination can never be greater than $R^2$. Therefore, the answer is never (option c).

The adjusted multiple coefficient of determination, also known as $R^2_{adj}$, is a modified version of $R^2$ that takes into account the number of independent variables and the sample size. It penalizes the inclusion of unnecessary variables in the model and adjusts $R^2$ accordingly.

The formula for
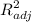`$R^2_(adj)$`j} =
`1 - (1 - R^2) \frac{{n-1}}{{n-k-1}}$`cient of determination, $n$ is the sample size, and $k$ is the number of independent variables. Option c