Question

a perpetuity pays 1 at the end of every year plus an additional 1 at the end of every second year. the present value of the perpetuity is k for i > 0. determine k.

Answer 1

Main Answer:

The present value (PV) of the perpetuity is
`\( k = (1)/(i) + (1)/(i^2) \) for \( i > 0 \).`

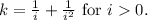
Step-by-step explanation:

The present value of a perpetuity is determined by summing the present values of each cash flow it generates. In this case, the perpetuity pays 1 at the end of every year and an additional 1 at the end of every second year. The formula for the present value of a perpetuity is
`\( PV = (C)/(i) + (C)/(i^2) \), where \( C \) is the cash flow and \( i \)` is the discount rate. In this scenario,
`\( C = 1 \) and \( i > 0 \)`. The first term
`\( (1)/(i) \)` represents the present value of the yearly cash flow, and the second term
`\( (1)/(i^2) \)` represents the present value of the cash flow every second year.

Combining these, the formula for the present value of the perpetuity is
`\( k = (1)/(i) + (1)/(i^2) \).` This equation represents the present value of all future cash flows generated by the perpetuity. To find the present value, one needs to solve fo
`r \( k \) when \( i > 0 \).` This expression captures the discounted value of both the yearly and biennial cash flows, providing a comprehensive measure of the perpetuity's present worth.