Question

X³ - 2x² - 35x = 0
Find all roots of the polynomial algebraically (not graphing)

Answer 1

The roots of the polynomial, the roots of the polynomial x³ - 2x² - 35x = 0 are x = 0, x = 7, and x = -5.

How to find he roots of a polynomial using algebraic method?

To find the roots of the polynomial x³ - 2x² - 35x = 0, you can factor it:

x(x² - 2x - 35) = 0

Now, you have two factors:

1. x = 0

2. x² - 2x - 35 = 0

For the quadratic factor, you can use the quadratic formula:

`x = (-b \pm √(b^2 - 4ac))/(2a)`

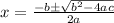
In the quadratic equation x² - 2x - 35 = 0, the coefficients are a = 1, b = -2, and c = -35.

`x = (2 \pm √((-2)^2 - 4(1)(-35)))/(2(1))`

`x = (2 \pm √(4 + 140))/(2)`

`x = (2 \pm √(144))/(2)`

`x = (2 \pm 12)/(2)`

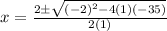
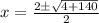
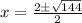
This gives two solutions:

a.
`x = (2 + 12)/(2) = 7`

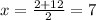
b.
`x = (2 - 12)/(2) = -5`

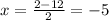
So, the roots of the polynomial are x = 0, x = 7, and x = -5.