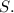Final Answer:
b. The function does not have a global maximum on S.
The question provides information about a critical point
 where the gradient of
where the gradient of
 However, without knowledge of the Hessian matrix and its definiteness at this point, we cannot determine whether it is a global maximum. Therefore, the function may not have a global maximum on
However, without knowledge of the Hessian matrix and its definiteness at this point, we cannot determine whether it is a global maximum. Therefore, the function may not have a global maximum on
 , leading to the selection of option b.
, leading to the selection of option b.
Step-by-step explanation:
In the given scenario, Alexander is maximizing a continuously differentiable function
 on the set
on the set
 The gradient of
The gradient of
 never vanishes inside
never vanishes inside
 and there is a unique solution
and there is a unique solution
 to the system of equations
to the system of equations
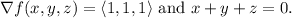
Now, to determine whether there is a global maximum on
 , we can examine the Hessian matrix. The Hessian matrix
, we can examine the Hessian matrix. The Hessian matrix
 is the matrix of second-order partial derivatives o
is the matrix of second-order partial derivatives o
 is positive definite at
is positive definite at
 has a local minimum; if negative definite, it has a local maximum. However, the question does not provide information about the definiteness of the Hessian, so we cannot conclusively state the nature of the critical point.
has a local minimum; if negative definite, it has a local maximum. However, the question does not provide information about the definiteness of the Hessian, so we cannot conclusively state the nature of the critical point.
Therefore, we cannot assert that the function has a global maximum at
 or anywhere else on
or anywhere else on
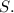 Thus, the correct answer is option b: The function does not have a global maximum on
Thus, the correct answer is option b: The function does not have a global maximum on