Question

newton and leibniz are co-founders of a tech startup that recently secured significant funding. they decide to invest their profits into two distinct portfolios, based on their risk appetite and investment strategies. newton puts $100,000 into a high-growth tech fund, which has been growing at a rate of 12% per year, compounded continuously. leibniz, on the other hand, invests $85,000 into a steady blue-chip fund, which is growing at a rate of 15% per year, but is only compounded quarterly. given their different investment strategies, calculate how long it will take until both their portfolios have the same value, assuming no additional deposits or withdrawals are made

Answer 1

It will take approximately 5.29 years for Newton and Leibniz's portfolios to have the same value.

Step-by-step explanation:

Newton and Leibniz have invested in two different funds with distinct compounding methods and growth rates. To determine when their portfolios will be equal, we can set up an equation equating the future values of their investments.

For Newton's investment in the high-growth tech fund, compounded continuously, the future value (FV) can be calculated using the formula:

`\[FV_N = P_N \cdot e^(rt),\]`

where
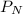`\(P_N\)` is the principal amount (initial investment), r is the annual interest rate, and t is the time in years. Substituting the given values, we get:

`\[FV_N = 100,000 \cdot e^(0.12t).\]`

For Leibniz's investment in the blue-chip fund, compounded quarterly, the future value can be calculated using the formula:

`\[FV_L = P_L \cdot \left(1 + (r)/(n)\right)^(nt),\]`

where n is the number of times interest is compounded per year. Substituting the given values, we get:

`\[FV_L = 85,000 \cdot \left(1 + (0.15)/(4)\right)^(4t).\]`

To find when the portfolios are equal, we set
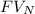`\(FV_N\)` equal to
`\(FV_L\)`:

`\[100,000 \cdot e^(0.12t) = 85,000 \cdot \left(1 + (0.15)/(4)\right)^(4t).\]`

Solving this equation, we find
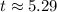`\(t \approx 5.29\)` years. Therefore, it will take approximately 5.29 years for both Newton and Leibniz's portfolios to have the same value.