Question

what is the speed of the block/bullet system after the collision? express your answer in terms of vi , mw , and mb . view available hint(s)for part c activate to select the appropriates template from the following choices. operate up and down arrow for selection and press enter to choose the input value typeactivate to select the appropriates symbol from the following choices. operate up and down arrow for selection and press enter to choose the input value type vf

Answer 1

The speed of the block/bullet system after the collision can be expressed as
`v_f = (m_b * v_i) / (m_b + m_w).`

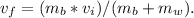
Explanation:

According to the principles of conservation of momentum in an isolated system, the initial momentum equals the final momentum. Initially, the bullet with mass m_b moves with a velocity v_i. After the collision, the combined mass of the block and the bullet is (m_b + m_w), and their combined velocity is v_f. Applying the conservation of momentum equation, where initial momentum equals final momentum, we have:
`m_b * v_i = (m_b + m_w) * v_f`. Solving for
`v_f`, we get
`v_f = (m_b * v_i) / (m_b + m_w).`

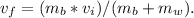
This equation signifies that the speed of the block/bullet system after the collision depends on the initial velocity of the bullet (v_i), the mass of the bullet (m_b), and the mass of the block (m_w). The numerator of the equation denotes the momentum of the bullet before the collision, while the denominator represents the combined mass of the block and the bullet after the collision.

Thus, the resulting velocity (v_f) depends inversely on the combined mass of the block and the bullet system, meaning a heavier combined mass would result in a lower final velocity. This calculation assumes an ideal scenario where no external forces act on the system during the collision, allowing for the conservation of momentum principle to hold true.