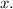Final Answer:
The demand function (price p as a function of units sold x) is
![\[ p(x) = -x + 12 \]](https://img.qammunity.org/2024/formulas/business/high-school/umzaucdbqe1bee14jmx4hdor4w1742gkks.png) .
.
Step-by-step explanation:
Let
 be the price function (in dollars) as a function of the number of necklaces sold
be the price function (in dollars) as a function of the number of necklaces sold
 . Since the demand function is assumed to be linear, it can be written in the form
. Since the demand function is assumed to be linear, it can be written in the form
 , where
, where
 is the slope and
is the slope and
 is the y-intercept.
is the y-intercept.
The problem states that when the price was $10, the sales averaged 20 per day. This point gives us the coordinates (20, 10) on the demand function.
Similarly, when the price was increased by $1, the average sales decreased by two per day. This corresponds to the point (18, 11) on the demand function.
Using these two points, we can find the slope
 of the demand function:
of the demand function:
![\[ m = \frac{{11 - 10}}{{18 - 20}} = -(1)/(2) \]](https://img.qammunity.org/2024/formulas/business/high-school/a9pkyjif7eyonm9qxl9b0mvihqbvuievl2.png)
Now that we have the slope, we can use one of the points (let's use
 to find the y-intercept
to find the y-intercept
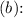
![\[ 10 = -(1)/(2)(20) + b \]](https://img.qammunity.org/2024/formulas/business/high-school/4qiw7duvxgps0vm8azewvuauiuxff1ogbl.png)
![\[ 10 = -10 + b \]](https://img.qammunity.org/2024/formulas/business/high-school/ukoyr79pc3wds8tk1en4a1nf8kdms87lab.png)
![\[ b = 20 \]](https://img.qammunity.org/2024/formulas/business/high-school/zcno0hi1637opx24ai84hfg1jstltebul5.png)
Therefore, the demand function is:
![\[ p(x) = -(1)/(2)x + 20 \]](https://img.qammunity.org/2024/formulas/business/high-school/i8zsb0zema7bhdp62fs4zu84anybyqd8t7.png)
To make it more convenient, we can multiply through by 2 to eliminate the fraction:
![\[ p(x) = -x + 40 \]](https://img.qammunity.org/2024/formulas/business/high-school/iputejuu2gwkca64jt9jitjh52vipsbp8b.png)
However, the demand function is typically written with a negative slope, so we can rewrite it as:
![\[ p(x) = -x + 12 \]](https://img.qammunity.org/2024/formulas/business/high-school/umzaucdbqe1bee14jmx4hdor4w1742gkks.png)
This represents the demand function where
 is the price in dollars as a function of the number of necklaces sold
is the price in dollars as a function of the number of necklaces sold