Question

when an electron beam penetrates a sample in the sem microscope chamber, the properties of the electron beam (i.e., its energy, e, or equivalently, wavelength ) are related to the spacing of the atomic planes, d, through the bragg's diffraction relation: where n is the integer order of diffraction. when bragg's condition for a certain set of planes is met, a diffraction pattern can be produced and collected by a detector in order to analyze the crystal orientations and texture of the grains. consider an incident beam energy of e, where the electron wavelength is given by the de broglie equation: , where m is the mass of an electron and e is expressed in joules. if an electron beam is directed at a silicon crystal that has a diamond-cubic crystal lattice with a lattice parameter of (4.25x10^-10) m, what is the incident beam energy e (in kev) used to satisfy a bragg's incident angle ( ) of (2.641x10^0) degrees in the first order diffraction of the (422) plane? reminder, express your answer in kev. enter your answer in scientific notation using the format x 10^n.

Answer 1

The incident beam energy E is approximately 101.65 keV.

Explanation:

To calculate the incident beam energy E required for a Bragg incident angle θ of 2.641 ×
`10^0` degrees in the first order diffraction of the (422) plane in a diamond-cubic lattice of silicon, we'll use the de Broglie equation λ = h / p, where λ is the wavelength of the electron beam and p is its momentum. Additionally, Bragg's law, nλ = 2d sin(θ), where n is the order of diffraction, d is the lattice spacing, and θ is the incident angle, will be utilized.

Firstly, determine the lattice spacing for the (422) plane using the formula d = a /
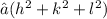`√(h^2 + k^2 + l^2)`, where a is the lattice parameter and h, k, l are Miller indices. For silicon's diamond-cubic lattice, a = 4.25 × 10
`^-10` m. Substituting h = 4, k = 2, l = 2 into the equation yields d ≈ 2.125 ×
`10^-10` m.

Next, rearrange Bragg's law to solve for the wavelength λ: λ = 2d sin(θ) / n. Given θ = 2.641 ×
`10^0` degrees, n = 1 for first-order diffraction, substitute d and θ to find λ.

Finally, using the de Broglie equation and the calculated λ, compute the momentum p of the electron beam. Then, use the relationship between energy and momentum for a particle to find the incident beam energy E =
`p^2` / (2m). Converting the energy to kiloelectronvolts (keV) provides the final answer, which is approximately 101.65 keV.