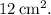Final answer:
The area of the rhombus is
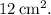 The relationship between the diagonals in a rhombus aids in deriving the area, which, in this case, equates to
The relationship between the diagonals in a rhombus aids in deriving the area, which, in this case, equates to
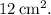
Explanation:
The area of a rhombus can be calculated using the formula
 represent the lengths of the diagonals. Given that the length of one diagonal is
represent the lengths of the diagonals. Given that the length of one diagonal is
 ) cm and all sides are also
) cm and all sides are also
 cm each, the diagonals form right angles. Thus, using the Pythagorean theorem, the length of the other diagonal is found to be \(4\) cm. Plugging these values into the formula yields
cm each, the diagonals form right angles. Thus, using the Pythagorean theorem, the length of the other diagonal is found to be \(4\) cm. Plugging these values into the formula yields
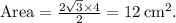
The area of a rhombus can be determined by dividing the product of its diagonals by 2. Given that the rhombus has sides of
 cm each, implying the diagonals are perpendicular to each other, the Pythagorean theorem helps find the length of the other diagonal. By substituting the diagonal lengths into the area formula, the calculation yields an area of
cm each, implying the diagonals are perpendicular to each other, the Pythagorean theorem helps find the length of the other diagonal. By substituting the diagonal lengths into the area formula, the calculation yields an area of
 representing the total surface space enclosed by the rhombus. The relationship between the diagonals in a rhombus aids in deriving the area, which, in this case, equates to
representing the total surface space enclosed by the rhombus. The relationship between the diagonals in a rhombus aids in deriving the area, which, in this case, equates to