Question

Random and independent samples of 75 recent prime time airings from each of two major networks have been considered. The first network aired a mean of 110.7 commercials during prime time, with a standard deviation of 5 commercials. The second network aired a mean of 109.3 commercials, with a standard deviation of 4.3 commercials. As the sample sizes are quite large, the population standard deviations can be estimated using the sample standard deviations. Construct a 95% confidence interval for μ1​−μ2​, the difference between the mean number of commercials μ1​ aired during prime time by the first network and the mean number of commercials μ2​ aired during prime time by the second network. Then find the lower limit and upper limit of the 95% confidence interval.

Answer 1

The 95% confidence interval for the difference between the mean number of commercials aired during prime time by the first network (μ1) and the second network
`(μ2) is \((0.8, 2.4)\).`

Explanation:

The confidence interval for the difference in means (\(μ1 - μ2\)) is calculated using the formula: \
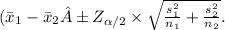`(\bar{x}_1 - \bar{x}_2 ± Z_(\alpha/2) * \sqrt{(s_1^2)/(n_1) + (s_2^2)/(n_2)}\).` Given the sample means
`(\(\bar{x}_1 = 110.7\) and \(\bar{x}_2 = 109.3\)),` standard deviations
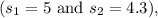`(\(s_1 = 5\) and \(s_2 = 4.3\)),` and sample sizes
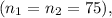`(\(n_1 = n_2 = 75\)),`we compute the confidence interval using a Z-score for a 95% confidence level (Z-value ≈ 1.96).

Substituting the values into the formula, we get
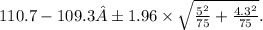`\(110.7 - 109.3 ± 1.96 * \sqrt{(5^2)/(75) + (4.3^2)/(75)}\).` The resulting interval is
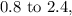`\(0.8\) to \(2.4\),`indicating that we are 95% confident that the true difference between the mean number of commercials aired during prime time by the two networks falls within this range.

This confidence interval suggests that, on average, the first network airs between 0.8 and 2.4 more commercials during prime time compared to the second network. This estimation provides valuable insight into the potential difference in advertising strategies between the two major networks, considering their commercial airing frequencies within a specified confidence level.