Question

There are k boxes that have been packed with m items each, and one defective item is among the km packed items. To try to find the defective item, n items from each box are randomly sampled.

Find the probability that the defective item is in box i. It is necessary to assume that the defective item is equally likely to be in each of the boxes.

To find the probability, divide the number of defective items, 1, by the number of items in a box, m. Therefore the probability is.

Answer 1

The probability that the defective item is in box
`\( i \) is \( (1)/(k) \)`.

Step-by-step explanation:

In this scenario, where
`\( k \)` boxes are packed with \( m \) items each, and one defective item is distributed among the \( km \) items, we need to determine the probability of the defective item being in a specific box
`\( i \).` Since we assume that the defective item is equally likely to be in each of the boxes, the probability is
`\( (1)/(k) \)`.

To understand this intuitively, consider that there is only one defective item distributed among the
`\( km \)` items, and each box contains \( m \) items. Therefore, the probability of the defective item being in a particular box \( i \) is the ratio of the number of defective items in that box (which is 1) to the total number of items in the box \( m \), resulting in \( \frac{1}{m} \). However, since the defective item is equally likely to be in any of the \( k \) boxes, we divide this probability by
`\( k \)`, yielding the final probability
`\( (1)/(k) \).`

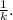
In mathematical terms, this can be expressed as:

`i) = (1)/(k) \]`

This conclusion holds under the assumption of an equal likelihood of the defective item being in any of the \( k \) boxes, providing a straightforward and concise answer to the given question.