Question

If two cards are randomly drawn (without replacement) from an ordinary deck of 52 playing cards, Z is the number of aces obtained in the first draw and W is the total number of aces obtained in both draws, find

(a) the joint probability mass function of Z and W
(b) the marginal probability mass function of Z
(c) the conditional probability mass function of W given Z = 1.​

Answer 1

Final Answers:

(a) Joint probability mass function of Z and W:

`\[ P(Z = z, W = w) = \begin{cases} \frac{{\binom{4}{z} \cdot \binom{48}{w-z}}}{{\binom{52}{w}}} & \text{if } 0 \leq z \leq w \leq 4 \\ 0 & \text{otherwise} \end{cases} \]`

(b) Marginal probability mass function of Z:

`\[ P(Z = z) = \sum_(w=z)^(4) P(Z = z, W = w) \]`

(c) Conditional probability mass function of W given Z = 1:

`\[ P(W = w | Z = 1) = \begin{cases} \frac{{\binom{3}{w-1} \cdot \binom{48}{1}}}{{\binom{51}{w}}} & \text{if } 1 \leq w \leq 4 \\ 0 & \text{otherwise} \end{cases} \]`

Explanation:

The joint probability mass function of Z and W represents the probability of getting z aces in the first draw (Z) and a total of w aces in both draws (W). This is calculated by considering the combinations of aces and non-aces in the deck. The probability is the ratio of favorable outcomes to the total possible outcomes, which is
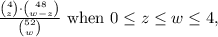`\(\frac{{\binom{4}{z} \cdot \binom{48}{w-z}}}{{\binom{52}{w}}}\) when \(0 \leq z \leq w \leq 4\),`and 0 otherwise.

The marginal probability mass function of Z is the probability distribution of Z alone, disregarding the specific values of W. It is obtained by summing the joint probabilities over all possible values of W, ranging from z to 4. This is expressed as
`\(\sum_(w=z)^(4) P(Z = z, W = w)\).`

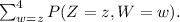
The conditional probability mass function of W given Z = 1 focuses on the probability distribution of W given that Z is equal to 1. It calculates the probability of obtaining w aces in both draws when one ace is already drawn in the first attempt. This probability is
`\(\frac{{\binom{3}{w-1} \cdot \binom{48}{1}}}{{\binom{51}{w}}}\) for \(1 \leq w \leq 4\)` and 0 otherwise, determined by the combinations of aces and non-aces in the remaining deck after drawing one ace.

These functions allow for a comprehensive understanding of the probabilities associated with drawing aces in a two-card draw scenario from a standard deck of 52 cards.