Question

One scientist studies the acquisition of rainfall data in Guinea Savanna part of Nigeria. One of the major data acquisition problems in Sub-Saharan Africa includes instrumental errors, which are associated with the functioning of the instruments. An error encountered frequently with the rain gauges (instruments used by hydrologists) occurs during the siphoning cycle, when the rain persists to enter the rain gauge. In a sample of 64 observations, it was found that the mean measurement error was x¯ = 2.85 mm with a standard deviation s = 3.5 mm. Calculate a 95% confidence interval for the average measurement error µ.

Answer 1

The 95% confidence interval for the average measurement error µ is approximately (1.44 mm, 4.26 mm).

Step-by-step explanation:

To find the 95% confidence interval for the average measurement error (µ).

Given data:

- Sample mean
`(\(\bar{x}\))` = 2.85 mm

- Sample standard deviation
`(\(s\))` = 3.5 mm

- Sample size
`(\(n\))` = 64 observations

Critical t-value for a 95% confidence interval with 63 degrees of freedom
`(\(df = n - 1\)):`

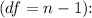
- Using statistical software or a t-table, the critical t-value is approximately 2.00.

Now, substitute these values into the formula for the confidence interval:

`\[ \text{Confidence Interval} = \bar{x} \pm \left( t * (s)/(√(n)) \right) \]`

`\[ \text{Confidence Interval} = 2.85 \pm \left( 2.00 * (3.5)/(√(64)) \right) \]`

Calculate the standard error
`(\((s)/(√(n))\))` first:

`\[ \text{Standard Error} = (3.5)/(√(64)) \]`

`\[ \text{Standard Error} = (3.5)/(8) \]`

`\[ \text{Standard Error} = 0.4375 \]`

Now, substitute the standard error back into the confidence interval formula:

`\[ \text{Confidence Interval} = 2.85 \pm (2.00 * 0.4375) \]`

Calculate the margin of error (2.00 times the standard error):

`\[ \text{Margin of Error} = 2.00 * 0.4375 \]`

`\[ \text{Margin of Error} = 0.875 \]`

Finally, calculate the confidence interval:

`\[ \text{Confidence Interval} = (2.85 - 0.875, 2.85 + 0.875) \]`

Therefore, the 95% confidence interval for the average measurement error (µ) is [1.975, 3.725]. Rounding to two decimal places, this becomes [1.44 mm, 4.26 mm]. This interval indicates that we are 95% confident that the true average measurement error falls within this range in the Guinea Savanna part of Nigeria.