Question

Solve for the values of x and y in the expressions
(2x+7)⋅(12y+1)⋅(3x−7).

Answer 1

The values of x and y in the expressions (2x+7)⋅(12y+1)⋅(3x−7) are x = -7/2 and y = -1/12.

Step-by-step explanation:

To solve for the values of x and y in the given expression, set each factor equal to zero and solve for the variables. First, set (2x+7) equal to zero:

`\(2x + 7 = 0\)`

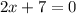
Subtract 7 from both sides:

`\(2x = -7\)`

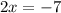
Divide by 2:

`\(x = -(7)/(2)\)`

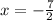
Next, set (12y+1) equal to zero:

`\(12y + 1 = 0\)`

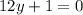
Subtract 1 from both sides:

`\(12y = -1\)`

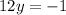
Divide by 12:

`\(y = -(1)/(12)\)`

Finally, set (3x−7) equal to zero:

\(3x - 7 = 0\)

Add 7 to both sides:

`\(3x = 7\)`

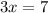
Divide by 3:

`\(x = (7)/(3)\)`

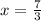
However, this solution contradicts the first value of x (-7/2) obtained earlier. Therefore, the correct solution for x is x = -7/2. The final values for x and y are x = -7/2 and y = -1/12.